Gerbang Logika (Logic Gate)

Gerbang Logika adalah rangkaian dengan satu atau lebih dari satu sinyal masukan tetapi hanya menghasilkan satu sinyal berupa tegangan tinggi atau tegangan rendah. Dikarenakan analisis gerbang logika dilakukan dengan Aljabar Boolean maka gerbang logika sering juga disebut Rangkaian logika.

Rangkaian logika sering kita temukan dalam sirkuit digital yang diimplemetasikan secara elekrtonik dengan menggunakan dioda atau transistor.

Ada 7 gerbang logika yang kita ketahui yang dibagi menjadi 2 jenis, yaitu :

1. Gerbang logika Inventer

Inverter (pembalik) merupakan gerbang logika dengan satu sinyal masukan dan satu sinyal keluaran dimana sinyal keluaran selalu berlawanan dengan keadaan sinyal masukan. Yang termasuk gerbang logika Inverter yaitu :

-Gerbang NOT

Inverter disebut juga gerbang NOT atau gerbang komplemen (lawan) disebabkan keluaran sinyalnya tidak sama dengan sinyal masukan.

A. Gambar gerbang NOT

B. Tabel Kebenaran NOT

Input (A)	Output (Y)
Rendah	Tinggi
0	1
Tinggi	Rendah
1	0

C. Fungsi gerbang (Persamaan Boolean) NOT
Y = NOT A   atau  . 
Misal : A = 1, maka = 0 atau Y = NOT 1 = 0
A = 0, maka = 1 atau Y = NOT 0 = 1

2. Gerbang logika non-Inverter

Berbeda dengan gerbang logika Inverter yang sinyal masukannya hanya satu untuk gerbang logika non-Inverter sinyal masukannya ada dua atau lebih sehingga hasil (output) sinyal keluaran sangat tergantung oleh sinyal masukannya dan gerbang logika yang dilaluinya. Gerbang logika non-Inverter antara lain :

-Gerbang AND

Gerbang AND mempunyai dua atau lebih dari dua sinyal masukan tetapi hanya satu sinyal keluaran. Gerbang AND mempunyai sifat bila sinyal keluaran ingin tinggi (1) maka semua sinyal masukan harus dalam keadaan tinggi (1).

A. Gambar gerbang AND

Gerbang AND dengan 2 Inputan

Gerbang AND dengan 3 Inputan

B. Tabel Kebenaran AND

Input (A)	Input (B)	Output (Y)
0	0	0
0	1	0
1	0	0
1	1	1

Dengan 2 Inputan

Input (A)	Input (B)	Input (C)	Output (Y)
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

Dengan 3 Inputan

-untuk mempermudah mengetahui jumlah kombinasi sinyal yang harus dihitung berdasarkan inputanya, gunakan rumus ini :

 2^n , dimana n adalah jumlah input. Contoh : n = 2 maka 2^2 = 4, jadi jumlah kombinasi sinyal yang harus dihitung sebanyak 4 kali.

C. Fungsi gerbang (Persamaan Boolean) AND 

Y = A AND B   atau Y = A . B  atau Y= AB  

Misal : A = 1 , B = 0 maka Y = 1 . 0 = 0
A = 1 , B = 1 maka Y = 1 . 1 = 1

-Gerbang OR

Gerbang OR mempunyai dua atau lebih dari dua sinyal masukan tetapi hanya satu sinyal keluaran. Gerbang OR mempunyai sifat bila salah satu dari sinyal masukan tinggi (1), maka sinyal keluaran akan menjadi tinggi (1) juga.

A. Gambar gerbang OR

Gerbang OR dengan 2 Inputan

Gerbang OR dengan 3 Inputan

Gerbang NAND juga disebut juga Universal Gate karena kombinasi dari rangkaian gerbang. NAND dapat digunakan untuk memenuhi semua fungsi dasar gerbang logika yang lain. 
 

B. Tabel Kebenaran OR

Input (A)	Input (B)	Output (Y)
0	0	0
0	1	1
1	0	1
1	1	1

Dengan 2 Inputan

Input (A)	Input (B)	Input (C)	Output (Y)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Dengan 3 Inputan

C. Fungsi gerbang (Persamaan Boolean) OR

Y = A OR B  atau Y = A + B 
Misal : A = 1 , B = 1 maka Y = 1 + 1 = 1
A = 1 , B = 0 maka Y = 1 + 0 = 0

-Gerbang NAND (Not-AND)

Gerbang NAND mempunyai dua atau lebih dari dua sinyal masukan tetapi hanya satu sinyal keluaran. Gerbang NAND mempunyai sifat bila sinyal keluaran ingin rendah (0) maka semua sinyal masukan harus dalam keadaan tinggi (1).

A. Gambar gerbang NAND

Gerbang NAND dalam arti logikanya

Gerbang NAND standard dengan 2 Inputan

Gerbang NAND dengan 3 Inputan

B. Tabel Kebenaran NAND

Input (A)	Input (B)	Output (Y)
0	0	1
0	1	1
1	0	1
1	1	0

 Dengan 2 Inputan

Input (A)	Input (B)	Input (C)	Output (Y)
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Dengan 3 Inputan

C. Fungsi gerbang (Persamaan Boolean) NAND

 atau  atau  
Misal : A = 1 , B = 1 maka  = 1 . 1 =  = 0


-Gerbang NOR (Not-OR)

Gerbang NOR mempunyai dua atau lebih dari dua sinyal masukan tetapi hanya satu sinyal keluaran. Gerbang NOR mempunyai sifat bila sinyal keluaran ingin tinggi (1) maka semua sinyal masukan harus dalam keadaan rendah (0). Jadi gerbang NOR hanya mengenal sinyal masukan yang semua bitnya bernilai nol.

A. Gambar gerbang NOR

Gerbang NOR dalam arti logikanya

Gerbang NOR standard dengan 2 Inputan

Gerbang NAND dengan 3 Inputan

B. Tabel Kebenaran NOR

Input (A)	Input (B)	Output (Y)
0	0	1
0	1	0
1	0	0
1	1	0

 Dengan 2 Inputan

Input (A)	Input (B)	Input (C)	Output (Y)
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

 Dengan 3 Inputan

C. Fungsi gerbang (Persamaan Boolean) NOR

 atau  atau 
Misal : A = 1 , B = 1 maka  = 1 + 1 =  = 0
-Gerbang XOR (Antivalen, Exclusive-OR)

Gerbang XOR disebut juga gerbang EXCLUSIVE OR dikarenakan hanya mengenali sinyal yang memiliki bit 1 (tinggi) dalam jumlah ganjil untuk menghasilkan sinyal keluaran bernilai tinggi (1).

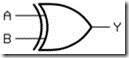
A. Gambar gerbang XOR 

Gerbang XOR standard dengan 2 Inputan

B. Tabel Kebenaran XOR

Input (A)	Input (B)	Output (Y)
0	0	0
0	1	1
1	0	1
1	1	0

Dengan 2 Inputan 

C. Fungsi gerbang (Persamaan Boolean) XOR

     atau  

-Gerbang XNOR (Ekuivalen, Not-Exclusive-OR)

Gerbang XNOR disebut juga gerbang Not-EXCLUSIVE-OR. Gerbang XNOR mempunyai sifat bila sinyal keluaran ingin benilai tinggi (1) maka sinyal masukannya harus benilai genap (kedua nilai masukan harus rendah keduanya atau tinggi keduanya). 

A. Gambar gerbang XNOR

 

Gerbang XNOR standard dengan 2 Inputan

B. Tabel Kebenaran XNOR

Input (A)	Input (B)	Output (Y)
0	0	1
0	1	0
1	0	0
1	1	1

Dengan 2 Inputan 

C. Fungsi gerbang (Persamaan Boolean) XNOR

      atau   atau